Math gets a bad rap, and it’s not entirely its fault. While some people may just not care for the subject, I believe math textbooks often fail to show students just how useful math can be. Their “real-world” problems often do not reflect realistic scenarios and instead rely on convoluted situations. If we approach math learning with more authentic and applicable lessons, we can change the way math is perceived and help students become truly invested in learning and practicing it. Let’s take a look at some flawed math problems that can prevent students from seeing the value of mathematics.
Problem #1:
Michaelangelo is in desperate need of some nickels and dimes for a candy machine. He asks Donatello, “How many nickels and dimes are in your pocket?” Donatello reaches into his pocket and finds 20 coins, all nickels and dimes, with a combined value of $1.75. Donatello challenges Michaelangelo: “You’re a supposed math ninja! You can figure out the number of each coin type by setting up and solving two equations.”
The above example, without the dialogue, is a classic real-world systems of equation problem found in many high school textbooks around the world.
But let’s be honest: you can’t seriously use it to answer, “When will I ever need algebra?” Could this overcomplicated scenario really motivate a student to write and solve equations? Probably not.
Worse yet, it would have been easier for Donatello to track the number of nickels and dimes when checking his pocket rather than calculating their total value.
Here’s a rule I live by:
- Never use high school algebra for a question you could answer through simple counting.
25 years ago I began a mission to bring real-world math into high school algebra. Often I was met with questioning looks. Aren’t nickels and dimes part of the real world? Over time it became clear to me: K-12 math teachers use the term “real-world” anytime there is a physical object in the problem. Nickels and dimes are “real”, so any problem that uses them is a real-world problem.
For me, real-world mathematics is “meaningful” mathematics, mathematics used to make actual decisions in their real-world work environment. Let’s investigate another problem that misses the mark.
Problem #2:
Joe’s school is selling tickets to the annual raffle. On the first day, the school sold 6 senior citizen tickets and 5 student tickets for a total $130. On the 2nd day, the school sold 12 senior citizen tickets and 13 student tickets for a total of $284. What is the price of each type of ticket?
If this was a true “real-world” scenario, why not just ask the ticket sales person or the booth manager for the prices? The lack of logic found in many of these problems means that we have no motivation to find the answer. So we’ve discovered another rule:
- Never use high school algebra to answer a question that someone already knows the answer to or does not need it.
What does an actual real-world math problem look like? Let’s take a look:
Simultaneous Equations in Realistic Context
A furniture company makes only two products: tables and chairs. The manufacturing of tables and chairs can be modeled using Lego pieces. A table requires two large and two small pieces, and a chair requires one large and two small pieces. Figure 2.0.1 shows a table and a chair made from Legos.
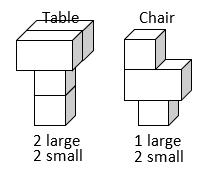
Suppose that the company can only obtain six large and eight small pieces per day.
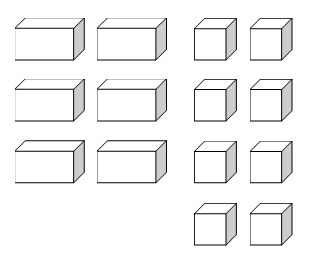
The question is, “How many chairs and tables can you produce and use all of the resources?”
X = Number of tables produced
Y = Number of chairs produced
2X + 2Y = 8 Number of Small Legos
2X + 1Y = 6 Number of Large Legos
The answer: Producing 2 tables and 2 chairs uses up all of the Legos.
This example is close to reality, a problem that a furniture company might actually encounter. I wish more math textbooks used this sort of problem! But since they don’t, I’ve opted to do it myself and strive to make learning easier, more enjoyable, and overall more useful to my students.
To take this example a step further and make it truly representative of decision making, in our next blog we’ll change the constraints into inequalities and add an objective: maximizing profit.

